Coming 'around' to sort out the game's lefties

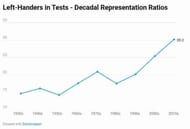
Lefties are a relatively new phenomenon in cricket. As recently as the 1950s, they made up only just more than 14% international Test cricketers, about 1% higher than the proportion of America's left-handed population. Placed against this background, it's palpable that rightie quick bowlers took a little over 80 years to identify the menace that they were and chose to apply the superior angle of operation from where since 2015 they average 10 less.

The advent of the West Indian pace quartet in the 1970s and their characteristic style precipitated a mass influx of left-handers into Tests.

But that's not all. Bowling from around the wicket is not an easy task. Illustrating the extent of this difficulty is tricky because we don't have direct access to the release coordinates of bowlers. This confines us to assuming the first thing about international cricket, like the neighbor next door, and that's what I did - take the point of the delivery of a bowler to be away from the stumps by one-sixth the pitch width.

That's 2.64 ÷ 6 = 0.44 meters, and the consequent diagram looks like this:

Right-arm fast bowler bowling over the wicket to right-hand batter (Source: author)

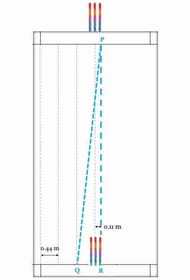
That's a right-arm fast bowler trying to hit a right-hand batter's off-stump from over the wicket. The release point is B, the interception point is A, and if you were to join A to C (the diametrically opposite stump), you get a right-angled triangle.

But point C is the off-stump at the bowler's end, and 0.44m is the distance between the middle stump at the same end and point B. Our triangle is useless as long as we don't know the dimensions of its sides. So here's what we did - the stump width prescribed by the MCC manual is approximately 22cm, meaning the distance between the middle stump and the off-stump is 11cm. We judiciously subtract these 0.11m from the block of 0.44m we have; that leaves us with BC = 0.33m.

What we're trying to find is the angle by which a bowler's bowling arm must be tilted to hit a particular line at the batter's end. Viscerally, that would be (90 − ∠ABC) degrees. The pitch length may be 22 yards, but the distance between the bowling crease and the batting crease is 17.68 m. So we know two sides of our triangle, and we need to find one of its angles. Enter trigonometry - ∠ABC turns out to be 88.57 degrees, the bowling arm's tilt 1.43 degrees.

Right-arm fast bowler bowling over the wicket to left-hander (Source: author)

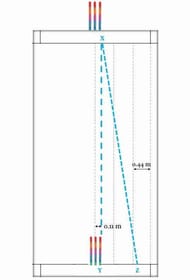
Let's keep that aside for a second. Here's a right-arm pacer hitting a left-handed batter's off-stump from over the wicket. The resultant triangle's base will be 0.44m + half the stump width, or QR = 0.55m. Again, we know the distance between the stumps, and we know the base of the triangle. So the angle subtended by the hypotenuse and the base turns out to be 88.21 degrees, and the bowling arm must be cocked away from the vertical by 1.79 degrees.

That's a difference of 0.36 degrees. Tilting the bowling arm by 0.36 degrees brings about a change in line by 22cm, about the same subtlety involved in trimming your beard with a shovel truck. For one, notice how miniscule a change this is. It's possible to formulate the change in tilt required to achieve a line differential of one meter (like a one meter change in length demands an 8 degree change in release point) but the final function comes out to be messy and bracketed depending on the lines you choose. But either way, what stands is that there's a vanishingly small difference between achieving off-stump to the right-hander and off-stump to the left-hander from over the wicket — perhaps one quite controllable.

Right-arm fast bowler bowling around the wicket to left-hand batter (Source: author)

Here's the around-the-wicket version of the same line. Your stodgily built right-arm pacer will bowl from the same spot (0.44m away from the stumps), but they'll have their body in between. This pushes away the the vertex of our triangle by whatever is the shoulder length of the bowler, which I've very dotingly chosen to be 50cm. The base of our triangle then turns out to be [0.44 + 0.50 − 0.11 (half stump width)] cm, which returns the measure of the angular tilt required to hit off-stump from around the wicket as 2.66 degrees in the opposite direction. That's −2.66 degrees.

On the face of it, this is not much. In absolute terms, it's less than twice the tilt required to hit the same spot for the right-hander from over the stumps. But the difference between that figure and this when you account for the change in direction from left-right to right-left is 4.09 degrees. That's more than 11 times the tilt difference required to bowl the same line from over the wicket against right-handers and left-handers.

If you bowl with the same tilt from over the stumps to a right-hander, you will be 0.83 meters away from the batter's off-stump. We'll hear an exasperated grunt from the wicketkeeper, resignation from the slips, and the police siren. Bowl it to the leftie from over the stumps and you'd have given away five wides. From the around-the-wicket angle, it's the perfect ball. It's what you've been sent to earth to do, your superhero pursuit; everything will be aglow with the light of a million fairies. For all your life you've been told to bowl anything but this ball against anybody; do anything else from the around-the-wicket angle to the leftie and you're an imperfect twiddler.

So Glenn McGrath bowled only 24% of his bowling to left-handers from around the stumps. It's hard, and you're unaccustomed to it and conditioned against doing it. But Kemar Roach bowls 93% of the times from here. For the longest time in history, the theoretical advantages of the around-the-wicket angle remained documented but left to rot in the books. Not anymore.

We live in an era in which batters are changing up their routines every 15 balls, bowlers are inventing new plans of action, touring teams are dominating home sides, and there are a dozen fast bowlers hitting the same lines over and over again rather than one. The draconian walls guarding information are slimmer and slimmer, Twitter is a womb of knowledge, and cricketers are listening to commentators more than ever. Ball tampering has been wiped off the surface yet the red ball swings all day long. None of that represents the biggest transformation of all.

Until 2015, your privileged left-hander averaged four runs more than the right-hander. Since then, he has averaged two less. The leftie's impact in Tests was so much that they came to represent a third of international male cricketers by 2015; now the quality of bowlers is so high that it's finally starting to go down.

Right-arm fast bowlers have finally come around the wicket in eighty years. And it's changed our game as we know it.